複雑な合成抵抗の問題を練習しよう
今回は、複雑な回路の合成抵抗の求め方(立体的な回路、線対称な回路など)について説明します！
複雑な合成抵抗の求め方にはいくつかパターンがあります。それは
- 回路を線対称に分ける
- 電流が通るルートを考え、電流が通らない導線は省く
の2つです。練習問題①～③が「回路を線対称に分ける」問題で、練習問題④が「電流が通るルートを考え、電流が通らない導線は省く」問題です。
「どういうこと？」と思っても大丈夫！一緒に考えていきましょう。
1.複雑な合成抵抗の問題
〇練習問題①
https://mgkca.com/question/similview/6267
〇練習問題②
問：図の抵抗Rはすべて60Ωである。AB間の抵抗は何Ωか。(第2種ME試験 第３０回 午前21)
〇練習問題③
問：R[Ω]の抵抗12個を図のように上下左右対称に接続したとき、ab 間の合成抵抗はRの何倍か。
https://mgkca.com/question/similview/6267
〇練習問題④
問：図に示すような抵抗の直並列回路がある。この回路に直流電圧5[V]を加えたとき、電源から流れ出る電流I[A]の値として、最も近いものを次の(1)～(5)のうちから一つ選べ。(電験三種 理論分野 平成25年 問8)
2.解答と解説
〇練習問題①
・解答
10[Ω]
・解説
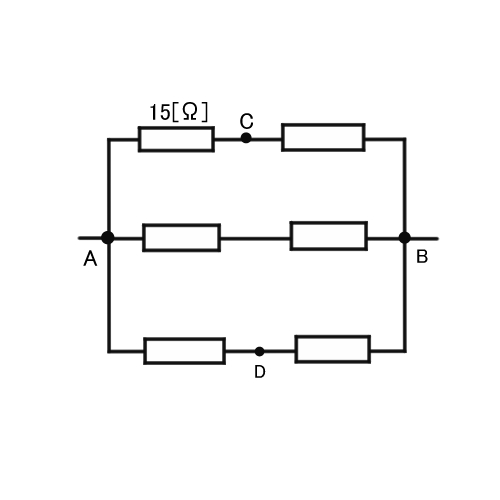
問題の図を真上から見た図を描いてみましょう。下の図のような形になるのは分かりますか？
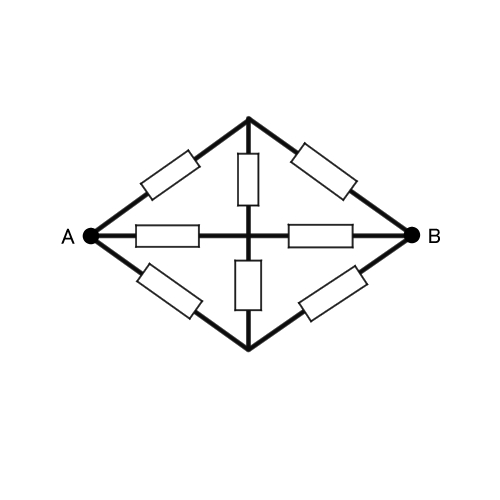
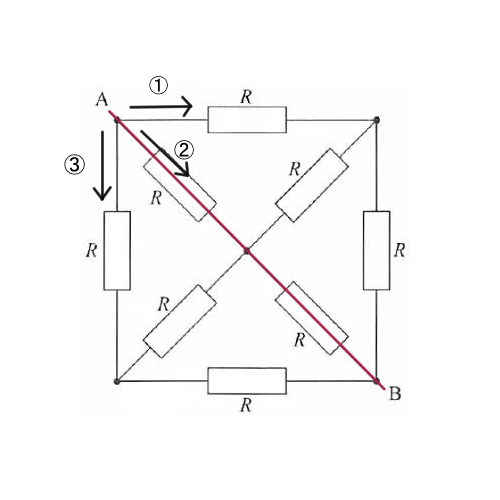
ここで、A点をスタート地点とした電流の流れがどのようになるのか考えてみます。
電流には、図形の線対称の部分に同じ分だけ流れるという性質があります。この場合、ABを対称にして考えると、①と③が線対称となるので、Aに流れ込んできた電流は、①と③にそれぞれ同じ分だけ流れます。ちなみに②には、(Aに流れ込んできた電流)ー(①と③に流れた電流)が流れます。
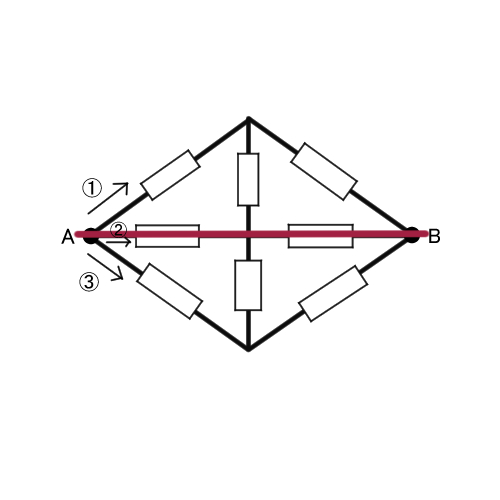
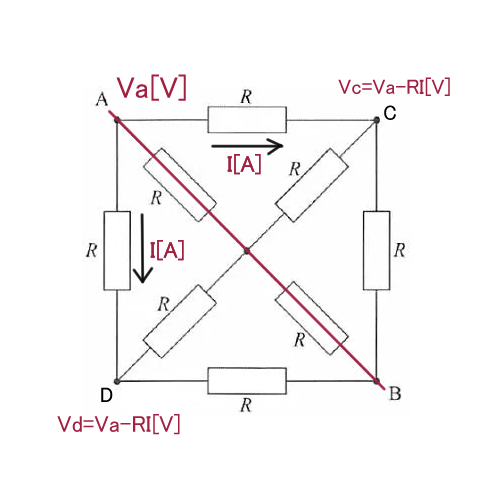
①と③に同じ電流が流れるということは、下の図の部分をC点とD点とすると、CとDは同じ電圧になります。 流れる電流も一緒で抵抗値も一緒なら電圧降下も同じになりますね！
CとDが同じ電圧ということは、CD間に電流は流れないということになります。つまり、CDに挟まれた抵抗器2つには電流は流れません。
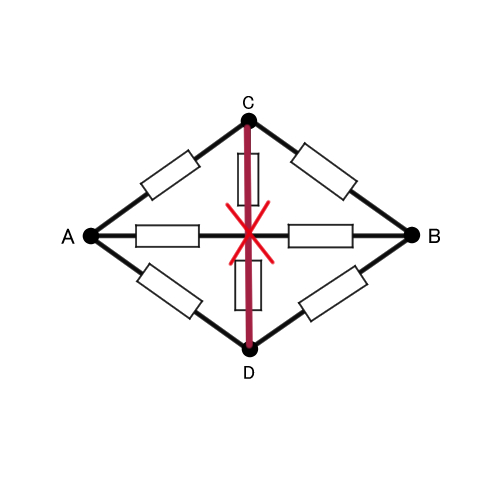
なので、CD間の部分は省いて考えることができます。
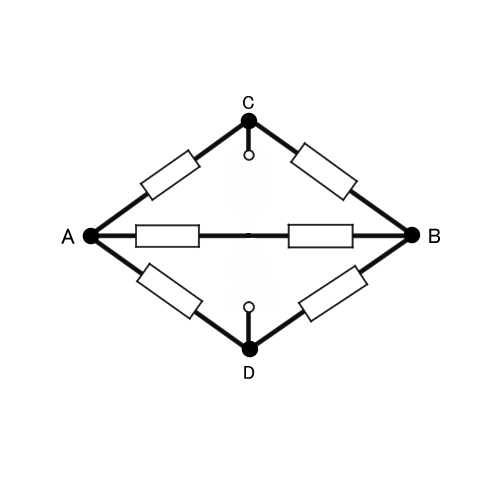
こうすれば、少しは考えやすくなるのではないでしょうか？1つの導線に2つの抵抗器がある並列回路になります。
まず、2つの抵抗値を1つにまとめると、それぞれ30[Ω]。まとめた抵抗器3つの合成抵抗は1/Ro=1/30+1/30+1/30より10[Ω]となります。
ちなみに、この問題ではAB間を軸にして考えましたが、CD間を軸にして考えるとどうなるのでしょうか？
もし、CD間を軸にして同じように考えると、AB間に電流が流れないことになってしまいます。
〇練習問題②
・解答
40[Ω]
・解説
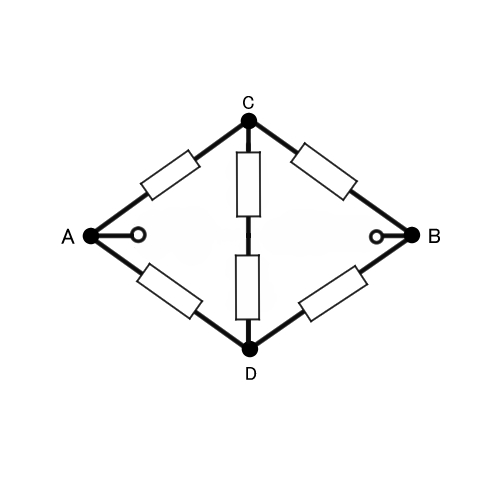
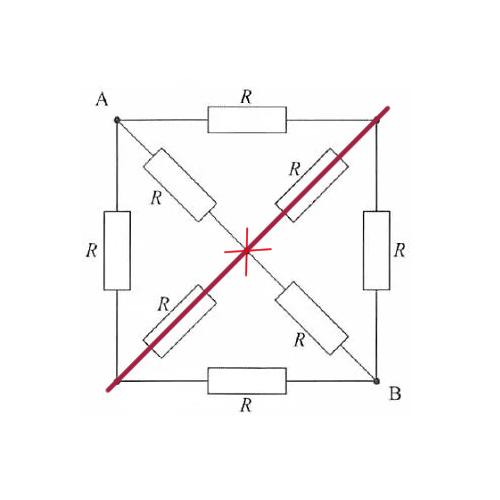
この問題も、練習問題①と同じような考え方で解いてみましょう。練習問題②は、立体的な図を真上から見た図になっています。
A点をスタート地点とした電流の流れがどのようになるのか考えてみます。練習問題①と同じようにAとBが通る線を対称にして考えると、①と③が線対称となるので、Aに流れ込んできた電流は①と③にそれぞれ同じ分だけ流れます。
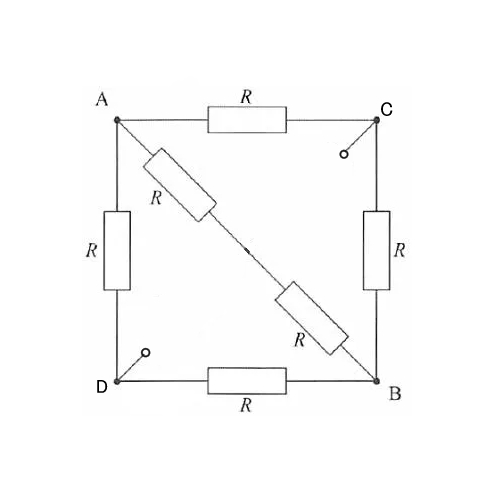
①と③に同じ電流が流れるということは、下の図の部分をC点とD点とすると、CとDは同じ電圧になります。
CとDが同じ電圧ということは、CD間に電流は流れないということになります。つまり、CDに挟まれた抵抗器2つには電流は流れません。
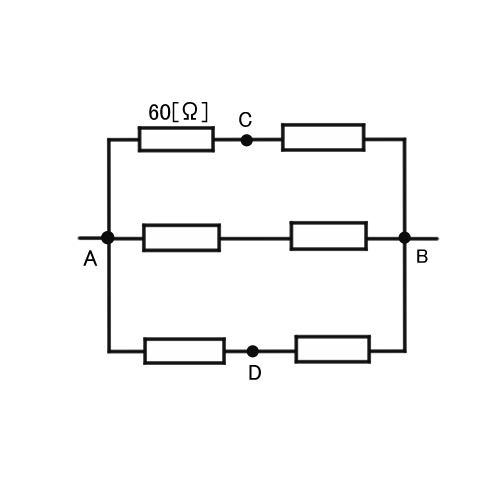
なので、CD間の部分は省いて考えることができます。
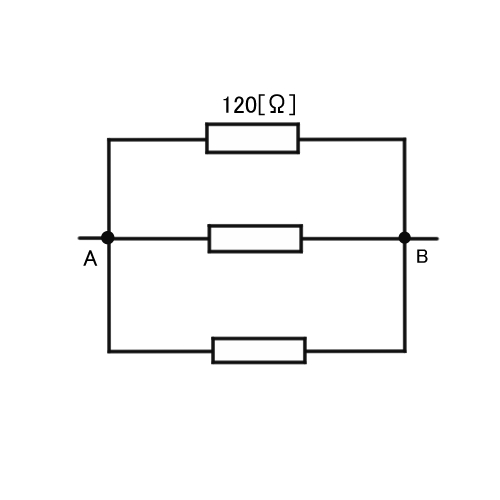
こうすれば、1つの導線に2つの抵抗器がある並列回路になります。
まず、2つの抵抗値を1つにまとめると、それぞれ120[Ω]。まとめた抵抗器3つの合成抵抗は1/Ro=1/120+1/120+1/120より40[Ω]となります。
〇練習問題③
・解答
1.5[倍]
・解説
この問題も、練習問題①や②と同じように線対称を使って考えますが、さらに複雑になっています。まず、aとbを軸として、抵抗を上半分と下半分に分けます。
上下に分けたら、ちょっと回路の形を分かりやすく変えてみましょう。真ん中の4つの導線が合わさっているところは同電位なので電流は流れず、導線はないものと考えることができます。
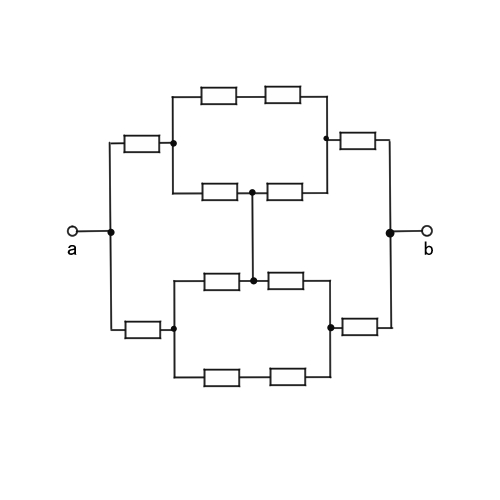
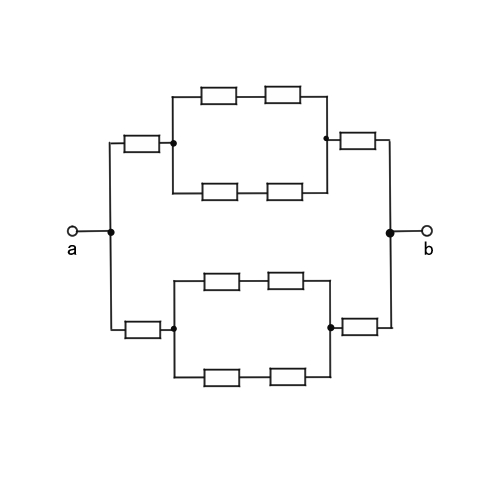
こうしたら、答えが見えてきませんか？上半分の合成抵抗を考えると、3R[Ω]。下半分も同じ形なので3R[Ω]。
上半分の合成抵抗と下半分の合成抵抗をそれぞれ1つの抵抗器にまとめてみます。すると、下のような単純な並列回路になるのは分かるでしょうか？
上の図の合成抵抗は1.5R[Ω]となり、Rの1.5倍になるので答えは1.5[倍]です。
〇練習問題④
・解答
(2)
・解説
この問題は「電流はどのようなルートで流れるか」を考えてみましょう。先に回路の合成抵抗を出してから、電源の5[V]で割って電流値を出します。
まず、電源から流れる電流は、40[Ω]と10[Ω]の二手に分かれます。
10[Ω]の抵抗に流れた電流は、その後抵抗のない導線に行きたいので、20[Ω]の抵抗には流れず、下方向の導線に流れます。
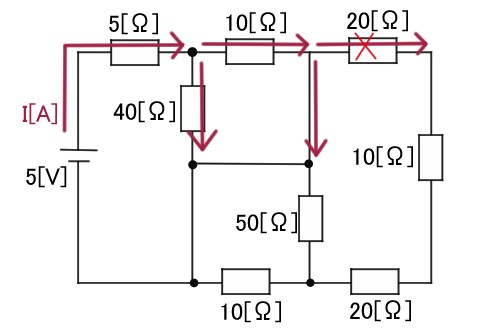
10[Ω]から下方向に流れた電流は50[Ω]の抵抗には流れず、左方向に流れます。
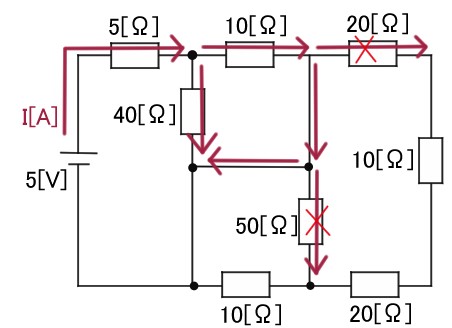
左方向に流れた電流は40[Ω]の抵抗から流れてきた電流と合わさって、下方向に流れます。そして、電源へと戻っていくのです。
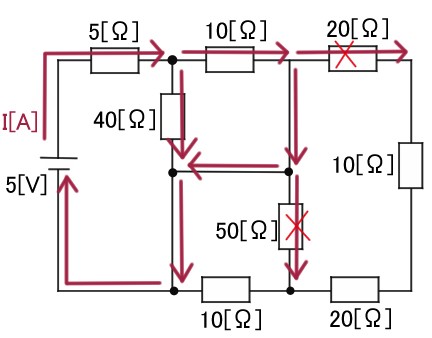
結局、電流が流れるルートをまとめると下の図のようになります。
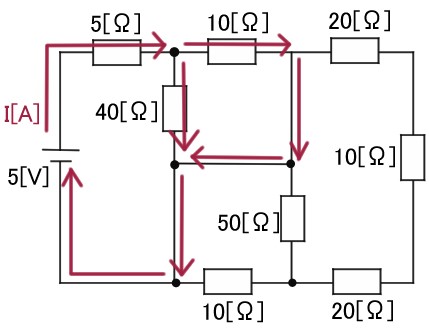
電流が流れるルートをもとに、回路を簡単に書き換えてみましょう。
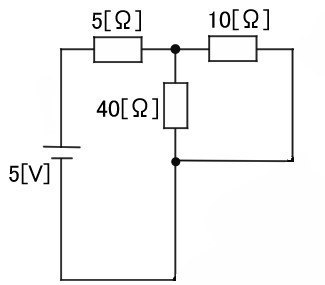
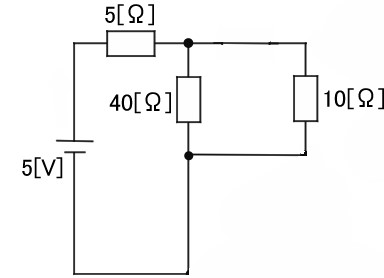
40[Ω]と10[Ω]は並列関係なので、2つの合成抵抗は8[Ω]。8[Ω]と5[Ω]は直列関係なので2つの合成抵抗は13[Ω]。流れる電流は、電源5[V]÷13[Ω]≒0.4[A]となります。
3.まとめ
複雑な合成抵抗を求めるときは、まず下の2つの方法を試してみればたいていの問題は解けるはずです。
- 回路を線対称に分ける
- 電流が通るルートを考え、電流が通らない導線は省く
