10分で分かるリミッタ回路の原理
今回は「ダイオードの基本的な原理」と「リミッタ回路の動作原理」についてお話しします。
リミッタ回路はダイオードの基本的な原理を理解し、入力電圧ごとに場合分けして考えれば解けるようになります。ちなみにリミッタ回路の出力波形はこんな感じ。
早速見ていきましょう。
「リミッタ回路の問題をもっと解いて練習したい！」という人は、問題だけを集めた「リミッタ回路の練習問題を解いてみよう！」という記事をご覧下さい。
1.ダイオードの原理
まずはダイオードの基本原理をおさらいしましょう。
〇順方向電圧
順方向電圧をかけるときはアノードの電位がカソードの電位より大きいときです。このとき抵抗は0[Ω]になりますから、1本の導線と同じような状態になり、普通に電流が流れます。
〇逆方向電圧
一方、逆方向電圧をかけるときは、カソードの電位がアノードの電位より大きいときです。このとき抵抗は無限大になりますから、導線が切れたのと同じ状態になります。つまり電流は流れません。
2.リミッタ回路の動作原理
リミッタ回路の基本的な動作だけ抑えておきましょう。
〇パターン1
パターン1では、下の回路にVi=Vmsinωt[V]を入力したときを考えます。
・Vi<E
電流が流れると仮定すると反時計回りに流れることになり、Dには逆方向電圧がかかります。よって断線と同じ状態になり、回路に電流は一切流れなくなります。すると抵抗の電圧降下はR×I=Vより0[V]になるので、抵抗部分はただの導線と化してしまいます。
その結果、b点を0[V]とおいて基準にして考えると、a点はVi[V]になります。
出力波形は下のように入力波形と同じになりますね。
・Vi>E
電流は時計回りに流れるのでDには順方向電圧がかかります。よってただの導線と化します。
b点を0[V]とおいて基準にして考えると、a点はE[V]になります。
出力波形は下のようになります。
・Vi<0
入力電圧がマイナスのときですね。
入力電圧がマイナスのときは、Viが-1[V]だろうと-2[V]だろうと電流は反時計回りに流れるので、Dには逆方向電圧がかかります。すると回路に電流は流れず、抵抗の電圧降下も0[V]なので、抵抗部分はただの導線と化してしまいます。
b点を0[V]とおいて基準にして考えると、a点は-Vi[V]になります。
出力波形は下のようになります。
パターン1での出力波形をまとめて書くと下のようになります。
〇パターン2(ダイオードとバイアス電圧の向きを反転)
つぎは、パターン1のDとバイアス電源の向きを逆にしたパターンです。
考え方はパターン1と同じで、Vi=Vmsinωt[V]を入力します。
・Vi>0
Viが1[V]だろうと2[V]だろうと電流は時計回りに流れるので、Dには逆方向電圧がかかります。すると回路に電流は流れず、抵抗の電圧降下も0[V]なので、抵抗部分はただの導線と化してしまいます。
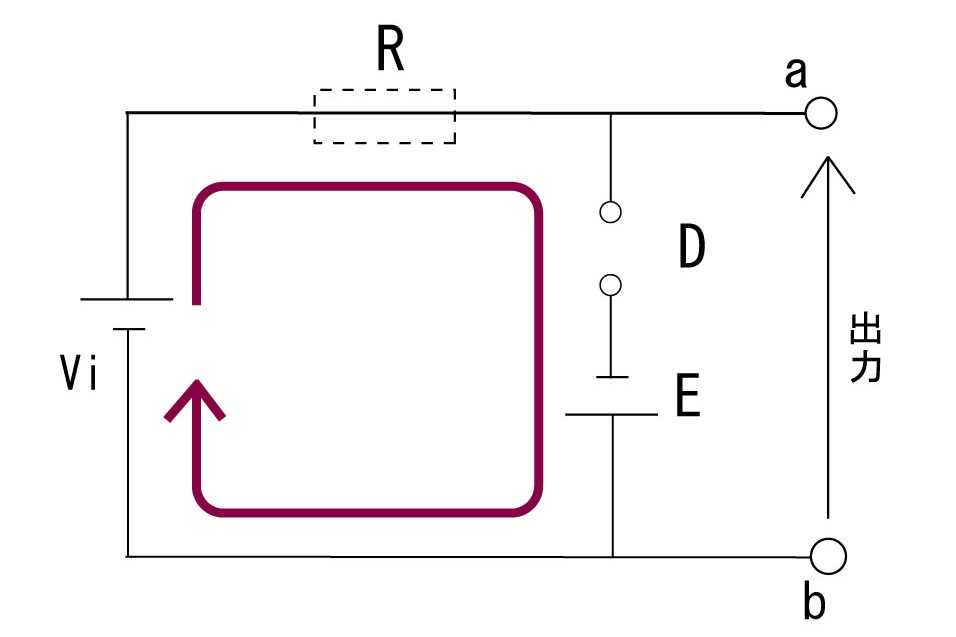
b点を0[V]とおいて基準にして考えると、a点はVi[V]になります。
出力波形は入力波形と同じになります。
・-Vi>-E
電流が流れると仮定すると、時計回りに流れることになり、Dには逆方向電圧がかかります。よって断線と同じ状態になり、回路に電流は一切流れなくなってしまいます。すると抵抗の電圧降下は0[V]になってしまうので、抵抗部分はただの導線と化してしまいます。
「-Viの方が大きいなら、電流は反時計回りに流れることになるのでは・・・？」と思った方もいると思いますが、電流は時計回りに流れます。
下の図は、回路の電圧の大きさの関係を分かりやすくするために回路を横から見た図です。
-Vi>-Eだから、b点を0[V]と置いて基準にしたら-E[V]より-Vi[V]の方が電位が高い（傾きが大きい）のが分かるでしょうか。
水はより高いところからの方が勢いよく流れるように、電流もより電位の高いところからの方が勢いよく流れるので、電流は時計回りに流れるんです。
b点を0[V]とおいて基準にして考えると、a点は-Vi[V]になります。
出力波形は下のようになります。
・-Vi<-E
電流の流れる向きは-Vi>-Eのときと同じように考えると、反時計回りに流れるのでDには順方向電圧がかかります。よってただの導線と化しますね。
b点を0[V]とおいて基準にして考えると、a点は-E[V]になります。
出力は-E[V]なので下のような波形になります。
パターン2の出力波形をまとめると下のようになります。
5.リミッタ回路のまとめ
上の2つの回路を組み合わせたような並列回路が出題されることが多いです。出力波形も、上の2つの出力波形を組み合わせたような波形になります。
リミッタ回路はダイオードの基本的な仕組みを理解し、入力電圧ごとに場合分けして考えれば解けるようになりますよ。
