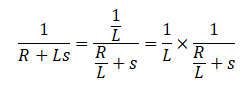ラプラス変換を使った過渡現象の解き方~直列回路編~

今回は、過渡現象を「ラプラス変換」を使って解く問題を紹介します。
微分方程式で解く方法は複雑ですが、ラプラス変換で解くと分かりやすいです。行程は長く感じるかもしれませんが・・・。
これまで、過渡現象の理屈もよく分かっておらず、なんとなく電流や電圧の式だけ暗記していた人は必見です!
1.ラプラス変換で過渡現象の問題を解く前に・・・
ラプラス変換で過渡現象を解くときは、暗記表を使って解きます。
過渡現象を解くときにわざわざラプラス変換の途中式まで書いていたら時間が足りなくなってしまいますからね。
過渡現象で用いるラプラス変換の公式はたいてい決まっているので、ここでは、過渡現象を解くときによく使うラプラス変換の公式を表にしてみました。

2.ラプラス変換を使って過渡現象を解いてみよう
〇問題:RL直列回路
問:図のRL回路において、スイッチSを閉じたときの電流i(t)をラプラス変換を用いて求めよ。


〇解説
①電圧に関する式を立てる
先に数値を入れて計算するのではなく、いったん式を作ってから数値を入れていきます。
まず、電圧に関する式を書きます。直列回路なので
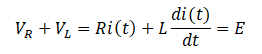
②両辺をラプラス変換
両辺をラプラス変換します。暗記表を見ながらやっていきましょう。

これより
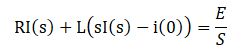
i(0)は初期条件の電流です。初期条件とは、ここではスイッチを閉じる1つ前の場面のこと。つまりスイッチが開いている状態の電流i(0)は0(A)ですよね。よって
![]() となり、i(0)が消えました。
となり、i(0)が消えました。
③「I(s)=○○」の形に書き換え
求めたいラプラス変換はI(s)についてなので、「I(s)=○○」の形に書き換えます。
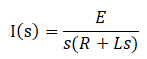
この式を部分分数分解すると
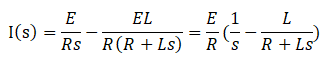
④逆ラプラス変換
ラプラス変換して出した式
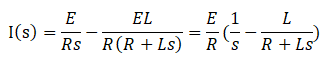
を逆ラプラス変換し、I(s)をi(t)に戻します。

よってI(s)を逆ラプラス変換すると
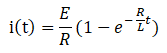 となります。
となります。
これに与えられている数値を当てはめて、
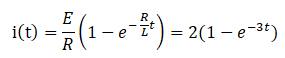
答えが導き出せました!
〇問題:RC直列回路
問:図のRC回路において、スイッチSを閉じたときの電流i(t)をラプラス変換を用いて求めよ。スイッチSをオンした時の時間をt=0[s]とする。スイッチSをオンする前には、コンデンサCに蓄えらえている電気量q(t)は0とする。

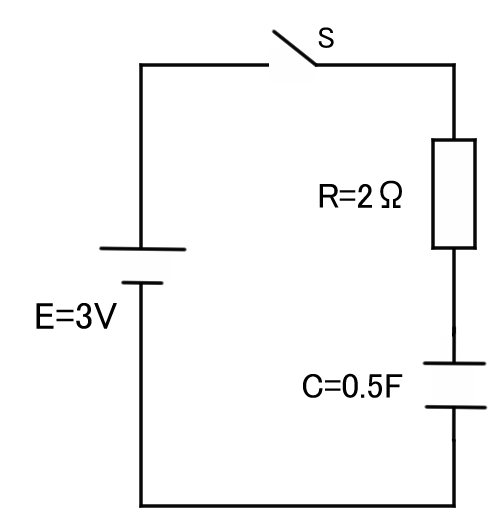
〇解説
①電圧に関する式を立てる
RL直列回路と同じように、数値の代入は後にして電圧に関する式を書きます。コンデンサの電圧はQ/Cです。コンデンサにたまる電気量Qは、時間が経つにつれて変化する時間関数なのでq(t)と表します。
![]()
②変数をi(t)にそろえる
ですが、RL直列回路とは違って「i(t)」と「q(t)」の2種類の関数が出てきました。
q(t)があると、ラプラス変換したときにI(s)=○○と表せないので、i(t)を求めることができません。そんな時は、q(t)をi(t)に変換して変数を全てi(t)にそろえます。
電流と電気量の関係を式で表すと
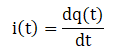 となります。
となります。
「電気量を微分すると電流になる」ということですね。
ということは、「電気量を微分すると電流になる」の逆は「電流を積分すると電気量になる」となります。
これを式で表すと、
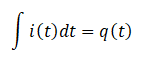
上の式を
![]() に代入すると
に代入すると
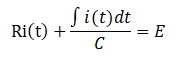 となり、変数がi(t)にそろいました。
となり、変数がi(t)にそろいました。
③両辺をラプラス変換
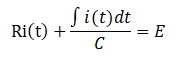 の式を、暗記表をもとにラプラス変換すると
の式を、暗記表をもとにラプラス変換すると
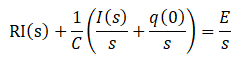 となります。
となります。
q(0)とは、スイッチを入れる1つ前の場面、つまりスイッチが開いている場面のときにコンデンサにたまっている電気量のことです。
問題文より、スイッチを入れる前の電気量は0なのでq(0)=0です。
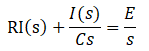
④「I(s)=○○」の形に書き換え
③の行程で導き出した式を「I(s)=○○」の形にします。
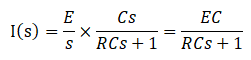
その後、1/(s+α)と似たような形に変形して、逆ラプラス変換しやすくします。
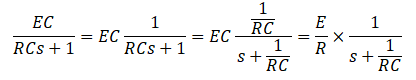
⑤逆ラプラス変換
④で導き出した式を、暗記表を基に逆ラプラス変換していくと、
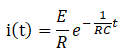 となります。
となります。
そして、問題文で与えられた数値を代入していきます。
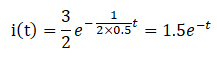
答えが導き出せました!q(t)が少し厄介ですが、電流と電気量の考え方を理解していれば解けます。
3.ラプラス変換を使った過渡現象の解き方のまとめ
ラプラス変換を使った過渡現象は、回路を流れる電流か電圧を求める問題がほとんどなので、以下の4つの手順を踏めば解けます。
何回も解いて練習しましょう!
ラプラス変換を使った過渡現象の問題(直列回路)も集めたのでぜひ見てみて下さい。
関連記事>>>ラプラス変換を使った過渡現象の練習問題~直列回路編~
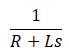 ・・・この形は暗記表に載っていないので、このままでは逆
・・・この形は暗記表に載っていないので、このままでは逆