ラプラス変換を使った過渡現象の練習問題～直列回路編～
今回はラプラス変換で過渡現象を解く問題の練習です。
関連記事>>>ラプラス変換を使った過渡現象の解き方～直列回路編～
実際に国家試験に出た問題を解いてみましょう！
1.問題：RL直列回路
問：図の回路でスイッチを閉じてから1ms後にインダクタの両端にかかる電圧[V]に最も近いのはどれか。ただし、白然対数の底eは2.7とする。(臨床工学技士国家試験 第31回 午前51)
〇解答
約0.6[V]
〇解説
まず、電圧に関する式を立てます。
両辺をラプラス変換して
i(t)=0より
「I(s)=○○」の形に変形して
I(s)を、ラプラス変換しやすいように変形します。
上の変形したI(s)式をを逆ラプラス変換して、
問題で与えられた数値を代入します。
インダクタの両端にかかる電圧を求めるのですが、抵抗の両端にかかる電圧の方が求めるのが簡単なので、まずは抵抗の両端にかかる電圧を求めます。
求める電圧は、スイッチを閉じてから1ms後の電圧なので、tに1m[s]を代入します。
「インダクタの両端にかかる電圧=電源電圧-抵抗の両端にかかる電圧」で求められるので
抵抗の両端にかかる電圧を求めてからインダクタの両端にかかる電圧を求めるときは、「インダクタの両端にかかる電圧=電源電圧-抵抗の両端にかかる電圧」の工程を忘れないようにして下さいね！
2.RC直列回路
問：図の回路のスイッチSを閉じて10ms後のVcに最も近い電圧は何Vか。ただし、スイッチを閉じる前、コンデンサには電荷は充電されていないものとし、自然対数の底eは2.7とする。(第2種ME試験 第37回 午前30)
〇解答
6.3[V]
〇解説
まず、電圧に関する式を立てます。
変数をi(t)に揃えたいので、q(t)をi(t)に変換します。
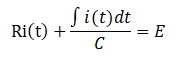
両辺をラプラス変換して
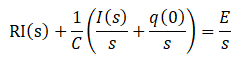
q(0)=0なので
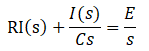となりますね。
そして、「I(s)=○○」の形に書き換え、
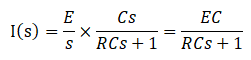
ラプラス変換しやすい形に変形します。
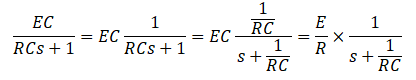
両辺を逆ラプラス変換して
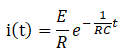
問題文で与えられた数値を代入して
まず抵抗の電圧の値を求めます。
t=10ms、e=2.7より、
求めるのはコンデンサの電圧で、コンデンサの電圧は電源電圧から抵抗の電圧を引くと求められるので、
